Sparse Signal Processing, Applications and Algorithms (summer semester)

This course focusses on the applications and algorithmic aspects of the compressed sensing in real-world problems. It consists of a series of seminars to be presented by us and by the students.

Although there are many interesting papers on the applications of compressed sensing, we have tried to select only those that provide fundamental insights into the compressed sensing problem and are easy to be read and be presented by the students. The students are supposed to select one of the papers in the list and present it in a session. The presentation should be intuitive enough so that the other students can follow. Moreover, at a technical level, the students should discuss some of the mathematical techniques applied in the paper. This would give an opportunity to the other students to see the concrete application of some of the mathematical tools developed during the last semester.

The first 4 weeks of the course will be covered by us. This will give the students enough time to read the paper and prepare their presentations. A tentative plan and a list of topics covered during the course is as follows:

1. The Convex geometry of linear inverse problems by V. Chandrasekaranm, B. Recht, P. A. Parrilo, and A. S. Willsky.

2. Kashin Splitting Theorem

   1. ‘‘A simple proof of Kashin's decomposition theorem’’ by S. Foucart.

   2. ‘‘The widths of certain finite-dimensional sets and classes of smooth functions’’ by B.S. Kashin, Izv. Akad. Nauk SSSR (Ser. Mat.), 41 (2) (1977), 334– 351, English transl.: Math. USSR-Izv., 11 (2) (1977), 317–333.

3. Low-complexity measurement and recovery

   1. RIP matrices with many 0's (sparse matrices)

   2. Expander graphs and 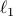-RIP

      1. ‘‘Efficient and Robust Compressed Sensing using Optimized Expander Graphs’’ by S. Jafarpour, W. Xu, B. Hassibi, R. Calderbank.

1. Recovery of individual signals

   1. Recovery guarantees for 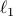-minimization via dual certificate.

   2. Applications in line spectral denoising

      1. ‘‘Atomic norm denoising with applications to line spectral estimation’’ by B. N. Bhaskar, G. Tang, and B. Recht.

2. Other recovery algorithms

   1. Weighted 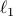-norm minimization

Further details: CommIT-TUB-website and ISIS/Moodle@TU-Berlin