Compressed Sensing Lectures (winter semester)

winter term 2018/2019: first lecture on November,2 2018!!

This course introduces the basics of compressed sensing (compressive sampling), sparse modelling and the sparse signal processing. We will mainly teach the mathematical tools necessary for analyzing the compressed sensing problems including probability theory, concentration of measure, convex optimization, etc. A summary of the topics covered in this course is as follows:

1. Introduction to compressive sampling

   1. signal representation in over-complete dictionaries

   2. sparse signal modeling

   3. comparison with traditional Shannon-Nyquist sampling

2. Introduction to algebraic structure of compressed sensing

   1. signal recovery via 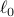and 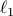minimization

   2. algebraic condition on the measurement matrix

3. Introduction to random matrices for compressed sensing

   1. necessary conditions for signal recovery under 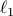minimization

   2. RIP (restricted isometry property) of the measurement matrix

Further details: CommIT@TU-Berlin and ISIS/Moodle@TU-Berlin